Binary Tree in C

A binary tree is a non-linear hierarchical data structure in which each node has at most two children known as the left child and the right child. It can be visualized as a hierarchical structure where the topmost node is called the root node and the nodes at the bottom are called leaf nodes or leaves.

In this article, we will learn the basics of binary trees, types of binary trees, basic operations that can be performed on binary trees as well as applications, advantages, and disadvantages of binary trees in C.

Representation of Binary Tree

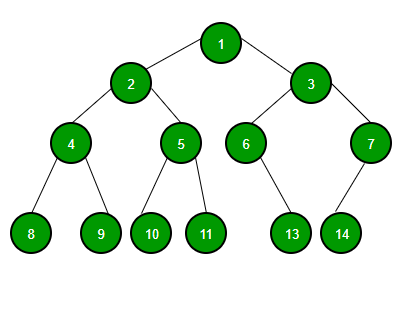
binary-tree-to-DLL

Binary Tree Representation

Each node of a binary tree has the following 3 parts:

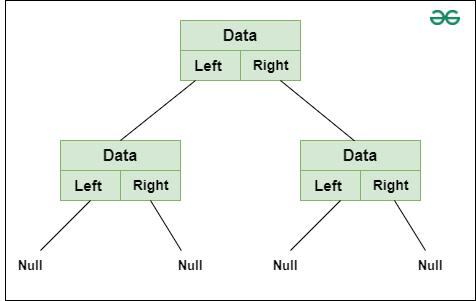
binaryTreeNodeRepresentation1

Binary Tree- Node Representation

To create a binary tree, we have to first create a node having a data, pointer to left child and pointer to right child using the below structure format:

struct node
 
int data; 
struct node *left; 
struct node *right;
>;

Basic Operations on Binary Tree in C

The following are the basics operations that can performed on a binary tree:

Here, we will learn about three basic operations that can be performed on a binary: insertion, deletion, and searching.

This function is used to insert values in a binary tree.

This function is used to delete the specified node from a binary tree

This function is used to search a given key in a binary tree

1. Insertion in Binary Tree

In a binary tree a new node can be inserted anywhere as a right child or left child of a node. To insert a node in a binary tree, follow the below approach:

Approach:

2. Deletion in Binary Tree

In a binary tree we can delete a node from anywhere and then again rearrange it to maintain the property of binary tree and the leaf nodes can be deleted without performing any replacement and shifting of nodes. To delete a node from a binary tree, follow the below approach:

Approach:

3. Searching in Binary Tree

In a binary tree we can search a node by traversing and comparing each node with target node (node to be searched). To search for a given node in a binary tree follow the below approach:

Approach: